「Excel(エクセル)で確率分布関数ってどう使うの?」
「二項分布、ポアソン分布、正規分布って何?」
データの分析や活用って年々重要になっています。
データを扱う上で求められることは以下の3つ。
- データを入手したときにどのような集計・分析を行うべきかを検討できる
- データ分析をした結果を理解し、コミュニケーションできる
- ビジネスの中でデータを使って意思決定を支援できる

ちょっと統計学とか難しそうなんだけど・・・
統計学って1つの学問ですが、確率分布とかなんやら難しそうですよね。
今回はそんな統計学について、エクセルの確率分布関数を使いながらご紹介します!
統計学って何?
そもそも、統計学って何でしょう?
統計学とは・・・
母集団からランダムに採取されたサンプルを調査し、平均や分散などの統計量から母集団の傾向や性質を理解する学問
ここでのキーワードが母集団とサンプルです。
調査をする上で全数調査したい対象のことを母集団、全数調査したい対象からランダムにピックアップして集めたデータがサンプルです。
例えば、商品の購買意欲や好き嫌いを調べたい場合、母集団:日本国民、サンプル:アンケートに答えた1,000人、といった具合になります。
では、なぜ統計学が大事なのかというと、母集団の傾向や性質に合ったビジネスプランや政策を立案することが出来るからです。
適材適所な方針を打つことで効率化が図れるってわけですね。
- 予測する
- 推計する
- 比較する
こういった時に統計学は役立ちます。
データを可視化しよう
データを扱う上で大事なこと、それはデータを正しく集計することです。
正しく集計できるとは、データが持つ特性を理解して、いくつかの数値やグラフで表現できる。
データが持つ特性とは、データの分布です。
ここで重要なキーワードが「分散」と「標準偏差」。
分散とは、データの散らばりの度合いを表す値です。
- 平均値を求める
- 偏差(データ - 平均値)を求める
- 偏差の二乗平均(=分散)を計算する
偏差とは、個々の数値と平均値との差のこと。個々のデータが平均値から偏っている程度を表しています。
標準偏差とは、データの散らばりの度合いを示す値です。
標準偏差を求めるには、分散の正の平方根を取ります。
データが平均値の周りに集中していれば標準偏差は小さくなり、逆に平均値から広がっていれば標準偏差は大きくなるのが特徴です。
確率分布を理解しよう
サンプルから母集団を理解するためには、確率分布が重要です。
確率分布とは・・・
確率変数が出る値とそれに対応する確率の値を表した分布のこと。
確率変数とは、「どのような値になるか」が確率的に決まる変数です。
例えば、コインを10回投げます。



10回全て表が出る確率は?
10回全てで表が出る確率は、(1/2)^10=0.001=0.1%
これは10回中全て表になるのが1通りになります。



では、5回表が出る確率は?
まず、5回表5回裏になるのは何通りあるのかを考えます。
これは、組み合わせの計算で10C5
10C5 x (1/2)^5 x (1/2)^5 = 0.246 = 24.6%
これを確率分布で表すと下図になります。
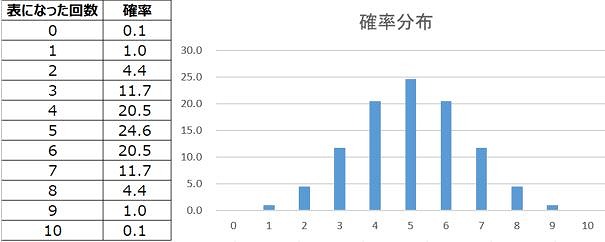

組み合わせの計算はエクセルで「=COMBIN(総数、抜き取り数)」で計算できます。
例えば、上記と同じように、10個のものから5個を抜きとる組み合わせの数は、「=COMBIN(10,5)」と入力します。
このコイン投げなど確率変数が回数や人数といった離散的なものについては『離散的確率』、確率質量関数といいます。
一方で、確率変数が重さや長さなど連続値の場合は『連続的確率」、確率密度関数というものもあるので注意。
全てのパターンを足し合わせると、確率は1になります。
また、確率分布はパラメーターと呼ばれる変数があり、そのパラメーターを変化させると形が変化することに注意。
3つの代表的な確率分布
確率分布には主に3つあります。
- 二項分布
- ポアソン分布
- 正規分布
「データがどの分布に従うか」は、データ分析の方向性を決める要素の1つになります。
二項分布とは?
二項分布とは、結果が二つの試行を何回も繰り返すことによって起こる分布のことです。
言い換えると、n回の試行のうち、確率pで起こるイベントの回数を表現するための分布です。
- n回のページビュー数のうち、確率pで広告がクリックされる回数
- n人のユーザーのうち、確率pで解約する人数
- n人の社員のうち、確率pで退職する人数
20回の試行で確率pをパラメータ(変数)として変化させると、二項分布の形はこんな感じになります。
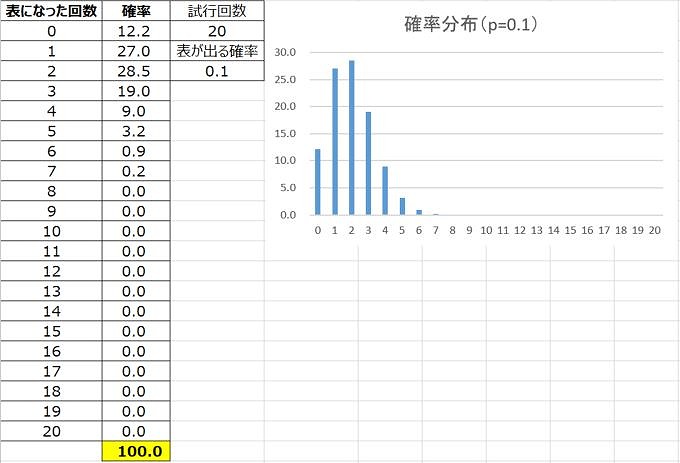

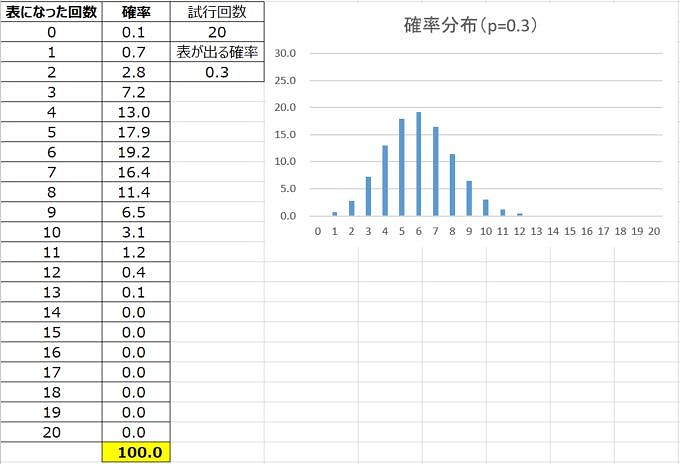

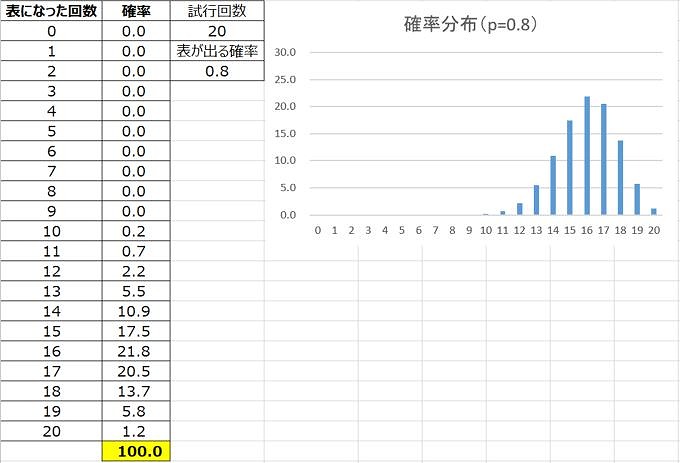

山の形が変化する、ということを把握することが大事。
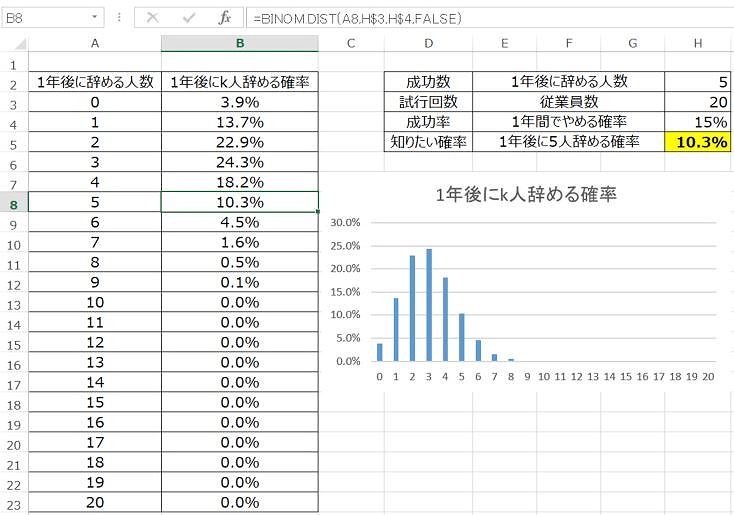
従業員が20人いる会社があったとします。1年間で一律15%の確率で従業員がやめるとすると、1年後に5人辞める確率は何%ですか?
ここでエクセルの関数を利用します。
エクセルでは「BINOM.DIST関数」を使うことで解くことが出来ます。BINOM.DIST関数は「=BINOM.DIST(成功数,試行回数,成功数,FALSE)」と入力することで計算されます。
*TRUE = イベント数0から指定したイベント数までが起こる確率の累積確率。
*FALSE = 指定したイベント数が起こる確率。
- 成功数:1年後に辞める人数
- 試行回数:従業員数
- 成功率:1年間で辞める確率
- 知りたい確率:1年後に5人辞める確率
エクセルで二項分布を作るとこんな感じになります。

ポアソン分布とは?
ポアソン分布とは、ある一定時間や一定空間内であるイベントが発生する回数を表現しています。
- 1ヶ月で平均n回コンバージョンする広告を使って得る今月のコンバージョン数
- 1日に平均n個の不良品が作られる工場で、今日作られる不良品の個数
そもそもポアソンとは数学者の名前なんですよね。
シメオン・ドニ・ポアソン(Siméon Denis Poisson、1781年6月21日 – 1840年4月25日)は、ポアソン分布・ポアソン方程式などで知られるフランスの数学者、地理学者、物理学者。
ポアソン-Wikipedia-
ポアソン分布では、「平均何回起こる」というパラメータ(変数)が重要になります。
ワードで文字をタイピングしていく中で、1枚につき平均4.5回の打ち間違えをするとします。1枚につき8回の打ち間違えをする確率は何%ですか?
ここでエクセルの関数を利用します。
エクセルでは「POISSON関数」を使うことで解くことが出来ます。POISSON関数は「=POISSON.DIST(イベント数,平均,FALSE)」と入力することで計算されます。
*TRUE = イベント数0から指定したイベント数までが起こる確率の累積確率。
*FALSE = 指定したイベント数が起こる確率。
- イベント数:1枚につき打ち間違えるとする回数
- 平均:打ち間違える平均回数
- 知りたい確率:1枚につき8回の打ち間違えをする確率
エクセルでポアソン分布を作るとこんな感じになります。


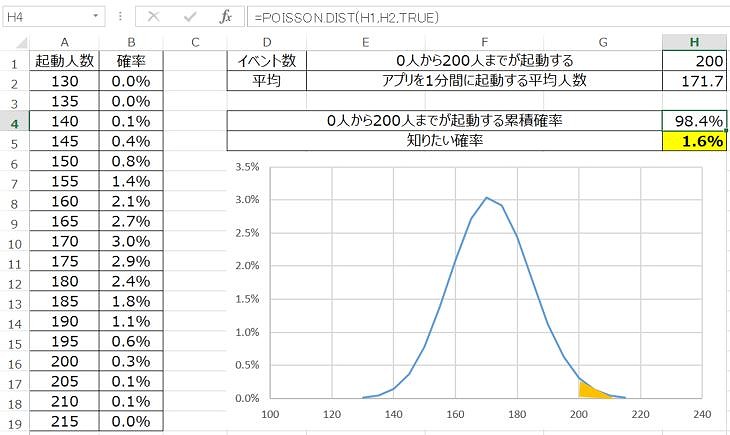
あるアプリを1分間に起動する平均人数は171.7人です。1分間に201人以上の人が同時に起動する確率はどの程度でしょうか?
ここで、エクセルのPOISSON関数を用いますが、ポイントは下記です。
全確率から0人から200人までが起動してしまう確率の累積を引いた確率が、導き出したい確率となります。
エクセルでは、「=1-POISSON.DIST(イベント数,平均,TRUE)」
*TRUE = イベント数0から指定したイベント数までが起こる確率の累積確率。
*FALSE = 指定したイベント数が起こる確率。
エクセルでポアソン分布を作るとこんな感じになります。

正規分布とは?
正規分布とは、ランダムな誤差を表す分布です。
- ある工場で製造される部品の寸法の誤差
- 証券や株の値段の不確実性
正規分布(Normal Distribution)は平均値付近に集まるデータの分布。
正規分布のパラメータは平均(μ:ミュー)と標準偏差(σ:シグマ)になります。
グラフで見ると、平均(μ:ミュー)が中心、標準偏差(σ:シグマ)が広がりを表すパラメータです。
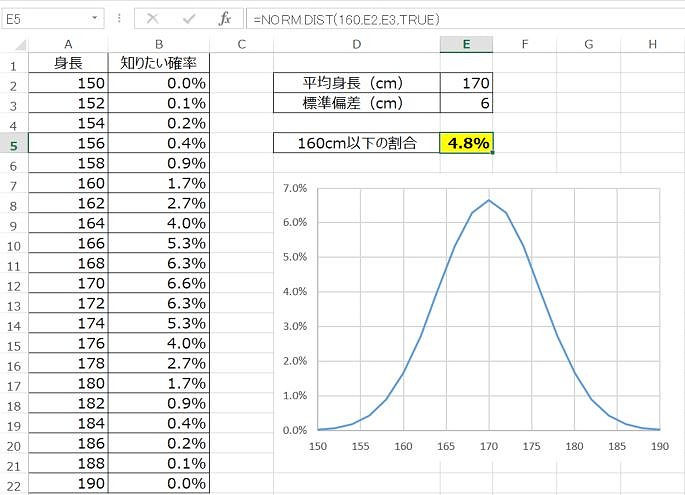
20歳日本人男性の身長の分布はほぼ正規分布にあてはまり、平均が170cm、標準偏差が6cmであるとします。そのとき身長160cm以下の人は、全体のどれだけいるでしょうか?
ここでエクセルの関数を利用します。
エクセルでは「NORMDIST関数」を使うことで解くことが出来ます。NORMDIST関数は「=NORM.DIST(変数,平均,標準偏差,TRUE)」と入力することで計算されます。
*TRUE = 指定した変数までが起こる確率の累積確率。
*FALSE = 指定した変数が起こる確率。
エクセルで正規分布を作るとこんな感じになります。

仮説検定で統計的に結論づけよう
仮説検定とは、統計的に結論づけること。
仮説検定を用いると、差異が偶然生じたものか、そうでないかを結論づけることができます。
- A/Bテストを行った結果、A案とB案に意味のある差異があったのかを結論づける
- マーケティング施策の前後で意味のある効果があったのかを結論づける
ただし、仮説検定は偶然の差異かどうかをチェックする手法であり、統計的に有意だからといって、必ずしも重要な発見であるとは限らないことに注意。
仮説検定で使われる仮説は2つあります。
- 帰無仮説
- 対立仮説
仮説検定は帰無仮説を「棄却」するために行います。
- 帰無仮説:商品AとBの売上は変わらない
- 対立仮説:商品Bが売れている
P値とは?
「棄却する」ために必要な考え方がP値(有意確率:Probability Value)です。
P値は帰無仮説が正しい確率のことを言います。
このP値が前もって定めた水準(有意水準:一般的には5%)より大きい場合は帰無仮説を採択し、水準より小さい場合には帰無仮説を棄却します。
- 帰無仮説と対立仮説を決める
- 有意水準を決める
- P値を求める
- 有意水準とP値を比べて帰無仮説を棄却するかを決める
P値の求め方
P値を求めるためには、下記数式を考えます。
(サンプル平均-母集団の平均)/(母集団の標準偏差/√サンプル数)
ただし、母集団の標準偏差は「分からないもの」なので、
(サンプル平均-母集団の平均)/(サンプルの標準偏差/√サンプル数)
というt分布により検定統計量tを求めます。
ここで、母集団の平均も「分からないもの」ですが、帰無仮説が正しいと仮定する場合、商品AとBの売上は変わらないので、母集団の平均を0とみなすことが出来ます。
すると、サンプル平均 /(サンプルの標準偏差/√サンプル数)により検定統計量tを求めることが出来ます。
- サンプル平均
- サンプルの標準偏差
- サンプル数
この3つが分かることで、検定統計量tを算出し、t分布における足切りライン(棄却域)と比較します。
エクセルでは「TINV関数」を使うことで足切りラインを計算することが出来ます。TINV関数は「=T.INV(確率,自由度)」と入力することで計算されます。
確率:一般的には片側検定だと95.0%、両側検定だと97.5%
自由度:サンプル数-1
検定統計量tを算出し、t分布における足切りライン(棄却域)に入る場合は、帰無仮説は棄却できます。
帰無仮説は1つの数字に定めるのがポイントです。
最初に立てた帰無仮説を正しいと仮定したうえで得られる確率分布において、データから得られる検定統計量が「めったに起こらない範囲(棄却域)」に入るか入らないかをチェックして結論づけることが出来ます。
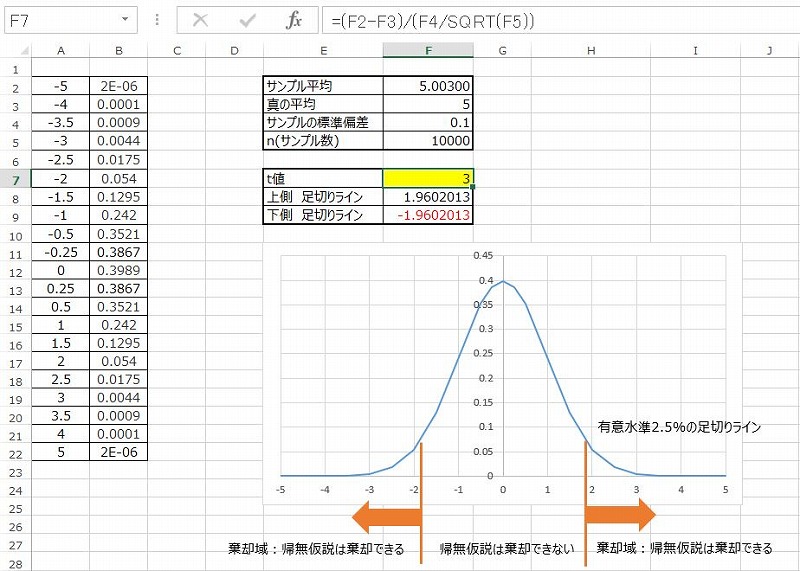
あなたはナット製造工場での生産管理を行っています。生産した5gのナットから10,000本をサンプリングし、帰無仮説を「ナットの重さの平均は5gである」、対立仮説を「ナットの重さの平均は5gではない」として仮説検定を実施することにしました。
サンプルの平均は5.003g、サンプルの標準偏差は0.1であった。有意水準を5%と設定したとき、仮説検定として正しいものを以下から一つ選びなさい。(ヒント: 両側検定であることに注意)
まず、t値を求めるには、(5.003-5)/(0.1/SQRT(10000)) = 3となります。
また、両側検定なので、棄却域は下側・上側それぞれに2.5%ずつ設定します。
その結果、下側の棄却域は-1.96以下、上側の棄却域は1.96以上となるため、t値は棄却域に含まれます。
t値は棄却域に含まれるので、帰無仮説「ナットの重さの平均は5gである」を棄却します。
「ナットの重さの平均は5gではない」ということが分かりましたね。
以上の例題はこんな感じでエクセルで解くことが出来ます。

さあ統計学を使ってみよう!
ビジネスで使える統計学についてご紹介しました。
専門用語や考え方が分かりにくいところもあるかとは思いますが、データの扱いについてもう一度おさらいしてみましょう!
- データを入手したときに、どのような集計・分析を行うべきか検討
- 伝えるべき数値が何であるか理解し、コミュニケーションする
- データを用いて意思決定を支援する
このようにしてビジネスではデータ活用をしていきます。
- 二項分布:1か0か、表か裏か、クリックするかしないかという場合
- ポアソン分布:一定時間や一定空間内で平均何回起きる中、それがレアな場合
- 正規分布:ランダムな誤差を表す場合
ぜひ、エクセルで確率分布関数を試してみてくださいね♪


コメント
コメント一覧 (2件)
お世話になります。確率分布関数のりけろぐを拝見しました。文系で統計数学をこれから学ぼうかとする者です。恐れ入りますが、最後のエクセル作業画面のB列のエクセル関数(正規分布関数???)の内容についてご教示下さい。宜しくお願いします。
とんくまさん、コメントいただきありがとうございます。
最後のエクセル作業画面とは、t分布でよろしいでしょうか?
最後のエクセル図では、例えばB2では『T.DIST(A2,$F$5-1,FALSE)』といった数式を使っています。
ご参考になれば幸いです^^